数理学習研究所、個別指導は、冬休み期間中下記の日程で行います。
冬休み中のみのご参加も大歓迎です。
| 月 | 火 | 水 | 木 | 金 |
| 12/22 9:00~12:00 |
12/23 | 12/24 9:00~12:00 |
12/25 9:00~12:00 13:00~19:00 |
12/26 9:00~12:00 13:00~16:00 |
| 12/29 | 12/30 9:00~12:00 13:00~19:00 |
12/31 9:00~12:00 |
1/1 | 1/2 |
| 1/5 9:00~12:00 |
1/6 9:00~12:00 13:00~19:00 |
1/7
14:00~19:00 |
1/8 9:00~12:00 13:00~19:00 |
1/9
13:00~19:00 |
※ その他、12月28日(日)および1月4日(日)は通常通り14:00~19:00の時間帯で承ります。
※ 1月11日以降は通常通りの日程で行います。(通常日程のご案内)
§ 形式
個別指導(同時に最大で3名まで)
§ 料金
入会費・年会費:なし
| 小学5年生まで | 2500円/時 |
| 小学6年生・中学生 | 3000円/時 |
| 高校生 | 3500円/時 |
| その他 | 5000円/時 |
(それぞれ、税別です。また、教材費は市販のものを使う場合、実費を徴収させていただきます。)
§ アクセス
豊島区南池袋2-47-6 パレス南池袋603
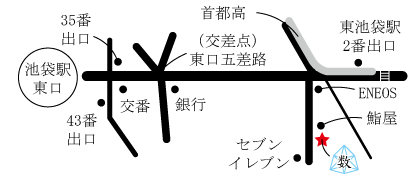
・池袋駅(JR,丸ノ内線,有楽町線,副都心線)からお越しの場合:徒歩8分
1) JR池袋駅東口、または、地下通路35番、または、43番出口を出る
2) 池袋駅を背に、大通りを直進(右側に交番がある大きな道です。少し行くと大きな交差点(東口五差路)がありますが、そこもそのまま直進します。)
3) ガソリンスタンド「ENEOS」の手前の道(「東池袋」の交差点)を右折
4) 道の左側、「パレス南池袋」と書かれた建物の、6階603号室です。(お寿司屋さんの隣、セブン-イレブンの斜向かいにある、グレーの建物です。1Fに、音楽スクールや歯科医院が入っています。)
・東池袋駅(有楽町線)からお越しの場合:徒歩4分
1) 2番出口をでて地上に
2) 目の前の大きな通りがあるので、横断歩道を渡り、右へ。
3) ガソリンスタンド「ENEOS」があるので、その奥の道を左折。
4) 以下、上記と同じです。
その他、雑司が谷駅(副都心線)からもお越しいただけます(徒歩10分)
§ お問合せ
toshihiro_oda@kurotake.net 宛にご連絡ください。
その際、どういった指導内容をご希望か、ご説明いただけるとありがたいです。
